秋田県令和２年度一般選抜学力検査問題の解説

はじめに。
昨今、理性的かつ合理的な手法で数学の問題が解ける生徒が富に減少しているようで残念に思っています。
　また、教える側の人間として、これまで何人かの生徒と接してきましたが、英語・国語はよくできるのに、数学がどうしてもうまくいかなくて第一志望校に進学できなかった生徒も幾人か目にしてきました。
　そこで今般、勉学に励む学生の皆さんの少しでもお役に立ちたいと考え、ここに私流の入試問題の解説を提供させていただきます。
　著作権法に抵触しない範囲で、実際に出題され、一般に広く公開されている入試問題を引用しながら、その下に私の解説をつけています。
熱意さえあれば、ほとんどの学生諸君が理解できるように、できるだけ理解が容易になるような解説に努めたつもりです。
学生の皆さんの数学に対する理解が深まることをお祈りしています。

大問１

（1）解説
この問題は計算の順番を問われる問題です。
数学はかけ算と割り算で構成されたブロックを計算した後に、たし算やひき算を計算して答えを出しますから、最初にかけ算部分の$(-0.2)×2$を計算した結果の-0.4に1を足して$+0.6=0.6$とします。
答え　0.6

（2）解説
分母と分子にそれぞれ$\sqrt{ 2 }$をかけ、分母を有理化した後に約分して答えにします。
$\displaystyle \frac{ 6 }{ \sqrt{ 2 } }=\frac{ 6 \sqrt{ 2 } }{ \sqrt{ 2 } \sqrt{ 2 } }=\frac{ 6 \sqrt{ 2 } }{ 2 }=3\sqrt{ 2 }$

（3）解説
a,bの各同類項をまとめてから値を代入したほうが簡単です。最初から式に代入してしまうと、a,bともかけ算を２回余計に計算しなければならないので面倒です。
$3(a-2b)-5(3a-b)=3a-6b-15a+5b=-12a-b$
$(-12)×\displaystyle \frac{ 1 }{ 2 } -3=-6-3=-9$

（4）解説
重さをきいていますから、各々の重さの合計≦20が成り立ちます。
$a$㎏の品物は３個で$a+a+a=3a$(㎏)、１個$b$㎏の品物は２個で$b+b=2b$(㎏)ですから、各々の重さの合計は$3a+2b$です。
したがって、 3a+2b≦20です。

（5）解説
「方程式を解きなさい」は、「方程式を成り立つときのxやyの値を求めなさい」ということです。また、方程式を成り立たせるxやyなどのことを解ということもありますから、 「方程式$\frac{ 2x+4 }{ 3 }=4$ の解を求めなさい」という問題になることもあります。このような問題が出たら何をすればいいのかしっかり理解しておきましょう。
分数と＝がある問題は、両辺に分数の分母の最小公倍数をかけて、分母を約分して１にすることを考えます。なぜならば、＝があるときは、＝の右と左（これを両辺といいます）になにか同じ数をかけても＝が成り立ち、分数が消えて式の計算が簡単になるからです。
両辺に３をかけると、
$\frac{ 2x+4 }{ 3 }=4$
$2x+4=4×3=12$
$2x=12-4=8$
$x=4$

(6)解説
代入法で求めます。
$2(-5y+4)-3y=-5$
$-10y+8-3y=-5$
$-13y=-5-8=-13$
$y=1$
下の式に代入して、
$x=-5×1+4=-1$
したがって、$x=-1,y=1$

（7）解説
解とは$x$のことですから、方程式に$x=1$を代入して$a$を求めます。
$1^2-2a+3=-2a+4=0$
$2a=-4$
$a=-2 $
次に $a=-2 $を方程式に代入してもう一つの解を求めます。
$x^2+4x+3=0$
$(x+3)(x+1)=0$
$x=-3,-1$
このことからもう一つの解は-3です。

（8）解説
往復ということは、家→博物館→家と往復しますから移動した距離は$2a$mです。また、行きは毎分60mで$a$mを移動していますから、かかった時間は道のり÷速さで$\displaystyle \frac{ a }{ 60 }$、同様に帰りは $ \displaystyle \frac{ a }{ 90 }$ です。つまり、往復の距離$2a$mを $\displaystyle \frac{ a }{ 60 }+ \frac{ a }{ 90 } = \frac{ 5a }{ 180 } = \frac{ a }{ 36 }$ (分)で移動しているので、 速さは、$ \displaystyle 2a(m)÷\frac{ a }{ 36 } (分)=2a× \frac{ 36 }{ a }= 72(m/分)$です。

（9）解説
「AはBである」、「AならばBである」の正誤を考える時はAとBの中に含まれる要素の数を考えます。AとBの要素の個数が等しいか、Bの要素の中にAの要素がすべて含まれていて、Bの要素の個数がAの要素の個数より多い時に「正しい」ということになります。
ア　逆は「すべての内角が等しい三角形は正三角形である。」
三角形はすべての辺と内角が等しい三角形ですから逆は正しいです。
イ　逆は「対角線がそれぞれの中点で交わる四角形は長方形である。」
正方形や平行四辺形も対角線がお互いを二等分する四角形ですから長方形とは限らないので逆は正しくありません。
ウ　逆は「 $x＞4$ならば $x≧5$である。」
例えば、4より大きい4.5は5以上ではありませんから逆は正しくありません。
エ　逆は 「$x^2=1$ならば$x=1$である。」
二乗して１になるのは１ばかりではなく、-１も二乗すれば１になりますから逆は正しくはありません。

（10）解説
鳳鳴を受けた塾生が言っていましたが、この問題は鳳鳴でも指定されなかったようです。毎年大問１の（10）は難問が多いので、ここは最初から手を付けず、後の問題を一通り解き終わって見直しをして、それでもなお時間が余った場合にのみ挑戦したらいいと思います。

$\sqrt{ 120+a^2 }$=m（mは整数）とします。
両辺を2乗して、$120+ a^2=m^2$から$m^2-a^2=(m+a)(m-a)=120-①$
かけて120になる数の組み合わせは(1,120),(2,60),(3,40),(4,30),(5,24),(6,20),(8,15),(10,12)の8組。-②
①と②からmとaの値を求めます。
$m+a=1,m-a=120$のとき、この二つの式をたすと$2m=121$、これはmが整数であることに矛盾します。
ここで気づくことがことがあります。
それは、たして奇数になる②の組み合わせは、すべてmが整数であることに矛盾するということです。
したがって①を満たすmとaの組み合わせは (2,60),(4,30),(6,20),(10,12)の4組であろうと予想がつきます。

1組ずつ検証していきます。
$m+a=2,m-a=60$のとき、$2m=62→m=31,a=-29$となりaが自然数であることに矛盾します。
でも、$m+a=60,m-a=2$と考えれば、m=31,a=29でaが 自然数、mが整数であることに矛盾しません。
ちなみにことのとき、$120+29^2=961=31^2$になります。
他の組み合わせも、同様に検証するとmは整数、aは自然数となります。
したがって 、$\sqrt{ 120+a^2 }$が整数となる自然数aは４個あります。

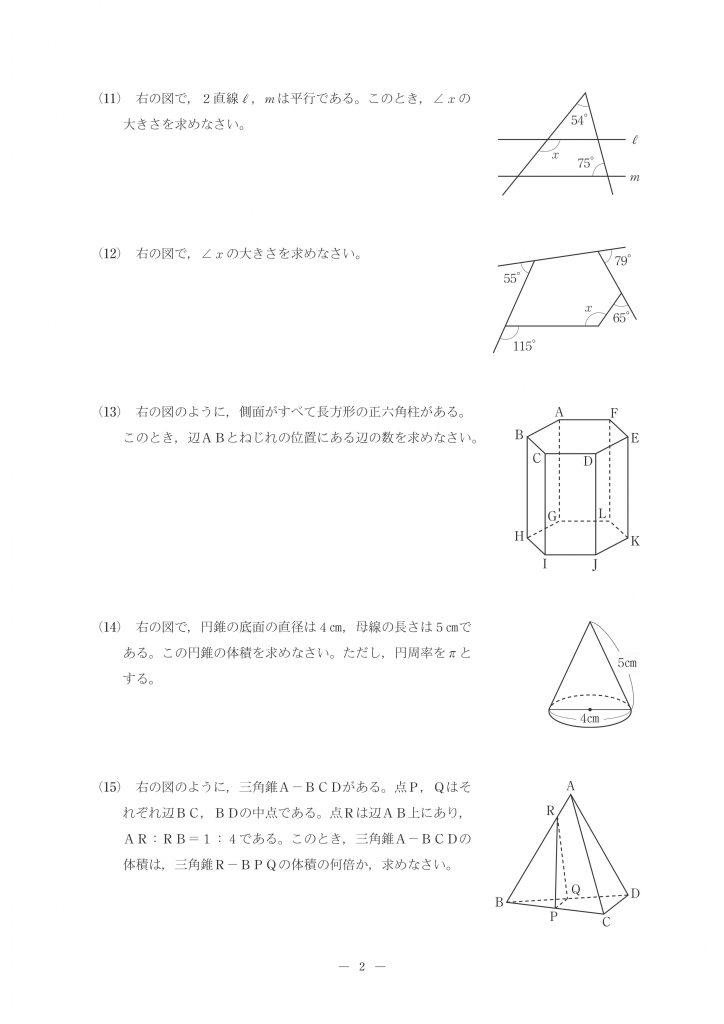
（11）解説
平行線の錯角は等しいので∠AED=75°
$x$は△ADEの外角だから$x=54°+75°=129°$

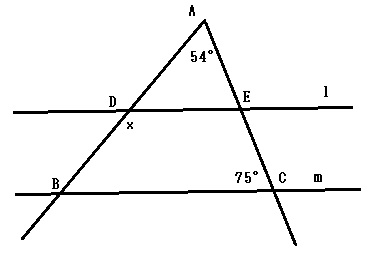
（12）解説
多角形の外角の和は360°だからxの補角（ 二つの角の和が180°になるとき、これらの二つの角を互いに補角をなすという ）は上の図から46°。
よって、x=180°-46°=134°

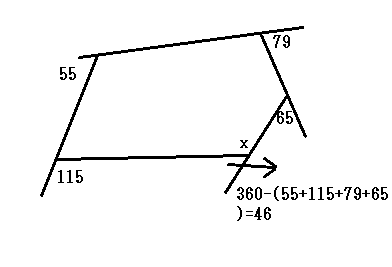
（13）解説
「辺ABとねじれの位置にある」とは、辺ABと交わることがなく、かつ平行な辺ではない位置にある辺です。ABと交わる辺と平行な辺は赤でマークした辺で、辺ABと合わせて10本あります。正六角形の辺の数は6×3=18本ですから、18-10=8本が答えです。

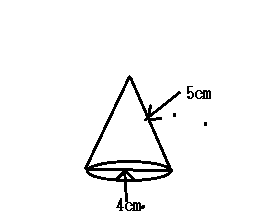
（14）解説
頂点から円の中心に下した垂線の足は底面の直径を2等分する。
底面の半径は2㎝だから三平方の定理から円錐の高さは$\sqrt{5^2-2^2 }= \sqrt{21 } $
したがって円錐の体積は、
$\displaystyle 2^2π× \sqrt{21 }× \frac{ 1 }{ 3 } =\frac{ 4\sqrt{ 21 } }{ 3 }π$（㎤）

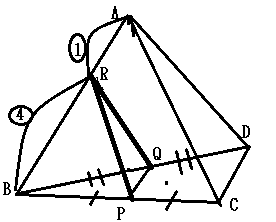
（15）解説
底面を⊿BCD、⊿BPQとみたときの 三角錐A-BCDと三角錐R-BPQの底面積と高さを考えます。
中点連結定理からPQ//CDで⊿BPQ∽⊿BCDは相似。相似比は1：2ですから、PQ：CD＝1：２から、 ⊿BPQと⊿BCDの面積比は$1^2:2^2=1:4 $。つまり⊿BCDの面積は ⊿ BPQ の面積の4倍になります。-①
また、 底面を⊿BCDとみたときのA-BCDの高さは、
⊿BPQを底面と見た場合のR-BPQ の高さの$\frac{ 5 }{ 4 }$倍です。 -②
①と②から 三角錐A-BCDの体積は、三角錐R-BPQの体積の $\displaystyle 4× \frac{ 5 }{ 4 }=5$倍になります。

大問2

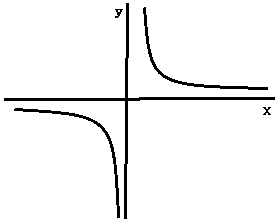
（1）解説
上のグラフから、x＜の範囲では、xの値が増加するとき、yの値は減少しています。また、 x＞0の範囲では、xの値が増加するとき、yの値は減少しています。このことからイとエが正解です。

(2)解説
①　㋐の$y=ax^2$は$P（6,9）$を通りますから、式に代入して$9=36a$。$\displaystyle a=\frac{ 1 }{ 4 }$。
このことから㋐は $\displaystyle y= \frac{ 1 }{ 4 } x^2$ですから、$x$に$-2$を代入すると、Qの$y座標b$は、$\displaystyle b= \frac{ 1 }{ 4 }×(-2)^2=1$。

②　$\displaystyle y=-\frac{ 1 }{ 2 }x^2$のyの変域が$-8≦y≦d$ですから、$yの最小値は-8$です。$y=-8$のとき $\displaystyle -8=-\frac{ 1 }{ 2 }x^2$から$x=±4$ですが、$x$の変域が$c≦x≦2$ですから$x=-4$であることがわかり、加えて$c=-4$であることがわかります。$-4≦x≦2$の範囲で、$y$は$-8$から徐々に増加して原点で最大値0となった後に減少に転じます。よってdは最大値であり$d=0$です。$-2$と答えた人は$d$が最大値を意味することをうっかり忘れています。

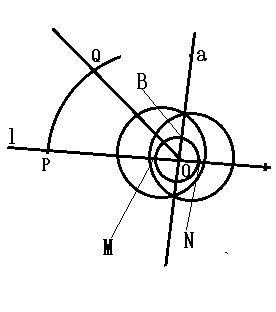
（3）解説
①コンパスで任意の長さを取って点Oを中心に円を描き、直線lとの交点を左からM,Nとします。
②コンパスで任意の長さを取り点Mと点Nを中心とする２つの円を描きます。
③二つの円の交点と点Oが一直線上に揃うことを確認しながら、点Oを通る直線$l$への垂線をひきます。 点Oを通る直線lへの垂線を直線$a$,直線$a$と円Oの交点を上から点B,点Cとします。
④コンパスで円Mの半径と同じ長さを取り、点bを中心とする円弧と円Mの円周との交点をみつけます。この交点をDとします。半直線ODをひきます。
⑤点Oを中心とする半径OPの円弧を半直線OD方向に描き、交点が求める点Qです。

(4)解説
平行四辺形は２組の対辺が平行で長さが等しいですから、錯角が等しいということで⊿FABと⊿FEDは相似な三角形、DEに対するABの比は３になります。結果として、相似な三角形は対応する辺の比が等しいのでAF：FE＝３：２になります。-①
対角線ACをひくと、AB＝CD、BC共通、平行四辺形の対角は等しいので∠ABC＝∠CDAから⊿ABC≡⊿CDAですから、平行四辺形ABCDの面積をSとすれば⊿CDAの面積は$\displaystyle \frac{ 1 }{ 2 }S$です。-①
ここで、ECを底辺と見た⊿AECとDCを底辺と見た⊿CDAの面積を比べてみます。
この二つの三角形は高さが同じですから、面積の比は底辺の比と等しくなり、⊿AEDの面積は ⊿CDAの面積の$\frac{ 2 }{ 3 } $です。
よって、①から⊿AEDの面積＝$\displaystyle \frac{ 1 }{ 2 }S × \frac{ 2 }{ 3 } ＝\frac{ 1 }{ 3 }S$です。 -②
同様に、今度はFEを底辺に見た⊿DFEとAEを底辺に見た⊿AEDの面積を比べてみます。
高さが同じで、底辺の比が⊿DFE：⊿AED＝2：5ですから、 ⊿DFEの面積は⊿AEDの面積の $\frac{ 2 }{ 5 }$です。
このことと②から ⊿DFEの面積 $＝ \frac{ 1 }{ 3 }S× \frac{ 2 }{ 5 }＝\frac{ 2 }{ 15 }$ となり、答えは $\frac{ 2 }{ 15 } $倍です。

大問３

(1)解説
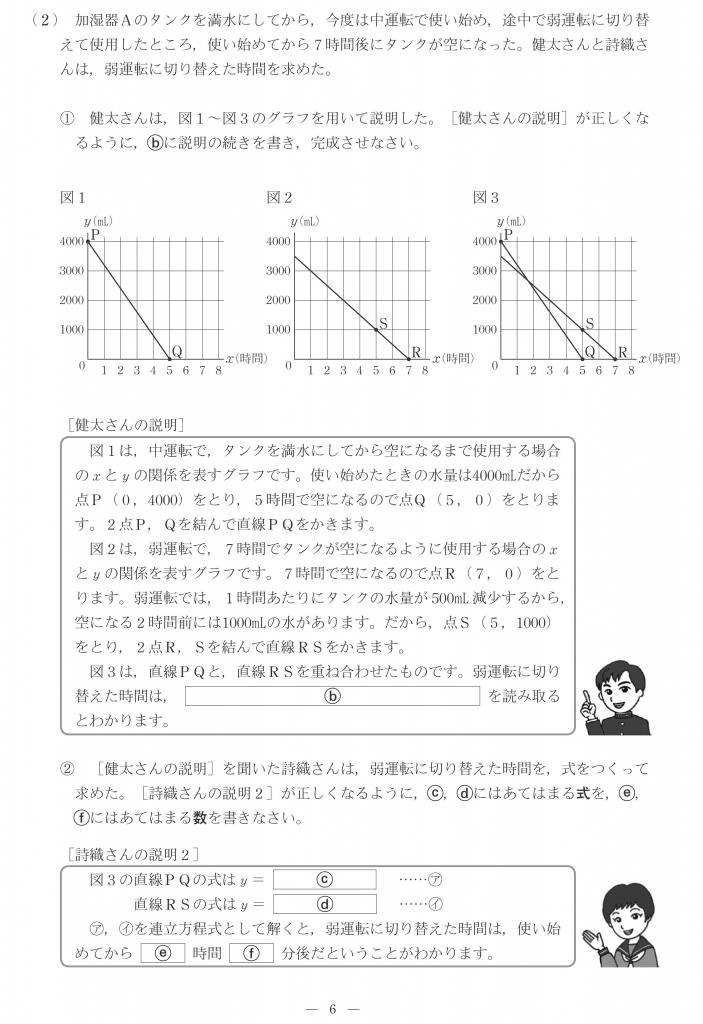
①強運転では4,000ｍLのタンクが4時間で空になりますから、1時間あたりにタンクの水量は4,000ｍL÷4時間＝1,000mL減少します。

②弱運転では1時間あたりタンクの水量は、4000÷8＝500mL減少します。グラフを見ると強運転から弱運転に切り替えた2時間後の時点で水は2000mL残っています。2000mLが1時間に500mLのペースで減少すると2000mL÷500mL=4時間後にタンクは空になります。ですから、(2,2000)と(6,0)の座標を結べばいいのです。

(2)解説
①のb　中運転の終わりと弱運転が始まりは、時間も残っているタンクの水量も同じです。このことから、直線ＰＱと直線ＲＳの交点のx座標を読み取ると弱運転に切り替えた時間がわかります。
ですからｂは「 直線ＰＱと直線ＲＳの交点のx座標」です。

②のc　 PQは(0,4000)と(5,0)を通っていますから、傾きが$\frac{ 4000-0 }{ 0-5 }=-800$で$y$切片が4000の一次関数で、ｃは$y=-800x+4000$。

②のｄ　PSは図２によると５時間から７時間まで２時間増加する間に1000mL減っていますから、傾きが$-\frac{ 1000 }{ 2 }=-500$で（7,0）を通る一次関数です。したがって0=-500×7+bからb=3500であり、ｄは$y=-500x+3500$。

②のe,f　ｃとｄの連立方程式の解の一つ$x$が答えです。㋐-㋑から、
$\displaystyle 0=-300x-500 →　300x=500 →x=\frac{ 5 }{ 3 }=1\frac{ 2 }{ 3 }=1\frac{ 40 }{ 60 }$
したがって、1時間４０分後が答えです。

大問４

（1）の解説
アとイ　最頻値とは「一番多い度数（この場合は回数）の属する階級値」のことです。また、階級とはある程度の幅を持った表現であり、〇以上～△未満と表現しますが、階級値とは（〇+△）÷２の値です。
これらのことから、アは一番度数が多い４回が属する階級から計算した階級値14.2、イは14.4となります。

ウ　14.2＜14.4ですからAさんの方が速く走れそうです。

（2）の解説
①大小２つのさいころを同時に投げる時の場合の数（すべての出目の組数）は、大のさいころの出目６通りそれぞれに小のさいころの出目が６通りあるので6×6=36通りです。
また、４の倍数になるa,bの組を考えると、
(a,b)=(1,4),(2,2),(2,4),(2,6),(3,4)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,4),(6,2),(6,4),(6,6)の15通りあります。
したがって、積abが４の倍数になるときの確率は$\frac{ 15 }{ 36 }$=\frac{ 5 }{ 12 }になります。

②最初に、２桁数の値が素数になるときのｂの値を吟味します。
２桁の数で1の位が偶数であれば、少なくても１,２,その数自体の３つの約数が存在するので素数ではありません。また、２桁の数で１の位が５の数は、１と５とその数自体の３つの約数を持つので素数ではありません。このことから、ｂは１と３だけに絞られます。
そこで、ab=11,21,31,41,51,61,13,23,33,43,53,63の中から素数を選ぶと８となり、素数になるときの確率は$\frac{ 8 }{ 36 }=\frac{ 2 }{ 9 }となります。

大問５

（1）の解説
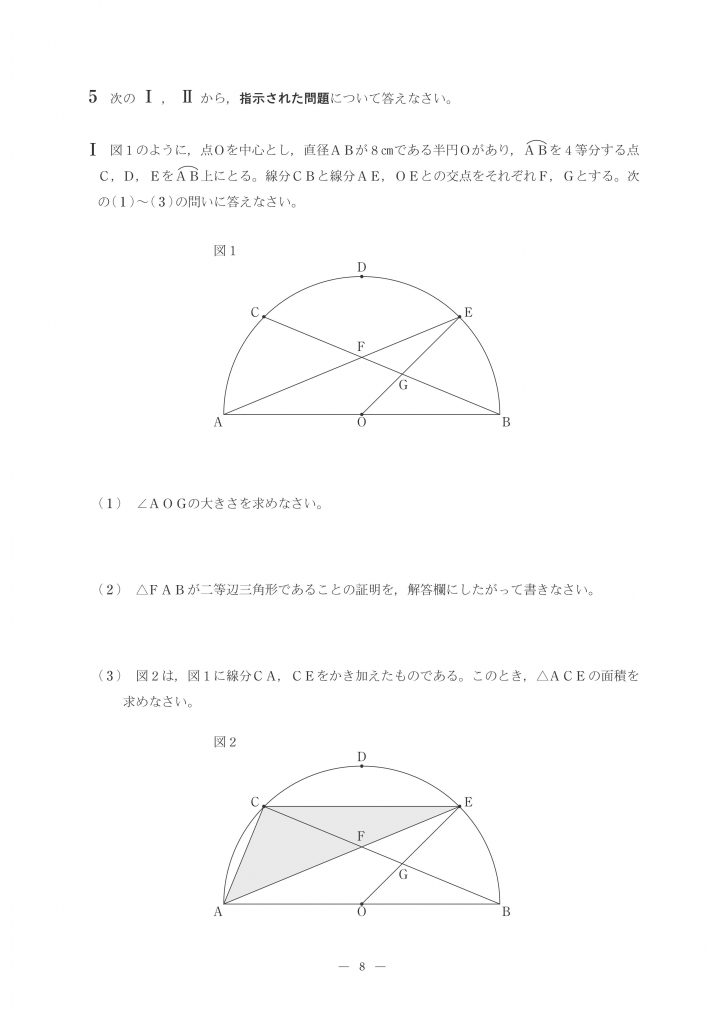
４等分されている弧の３つ分の中心角ですから、
（180°÷4）×3=135°

（2）の解説
⊿FABにおいて、
仮定から弧AC=弧BE
等しい弧に対する円周角は等しいから∠EAB=∠CBA
これにより、Fを頂点とする⊿FABの底角が等しいので、⊿FABは二等辺三角形である。

（3）の解説
∠COAと∠EOBは180°を４等分した角だからどちらも45°。-①
このことから∠COE＝90°。
COとOEは円の半径だから長さはどちらも4㎝。
したがって、⊿OCEの面積は$4×4×\frac{ 1 }{ 2 }=8(㎠）$
また、⊿OCEは二等辺三角形だから、∠OCE=（180-90）÷2＝45°
このことと①から錯角が等しいのでCE//AB。
よって、等積変形により⊿OCEと⊿ACEの面積は等しいので、⊿ACEの面積は8（㎠）

Ⅱ解説
（1）⊿HOBにおいて、
∠DBA=∠DOA÷2＝180÷6×2÷2＝30°（円周角は中心角の半分だから）
∠GOB=180÷6=30°
よって、Hを頂角とみたときに二つの底角が等しいので⊿HOBは二等辺三角形である。

（2）HからOBにおろした角の二等分線とOBの交点をJとする。
二等辺三角形の頂角の二等分線は底辺を垂直に２等分するから、OJ=3。
⊿OJHは辺の比が$1：2：\sqrt{ 3 }$の直角三角形だから、OJ:OH＝$ \sqrt{ 3 }：2$
つまり、$\displaystyle OH＝\frac{ 2 }{ \sqrt{ 3 } } ×3=\frac{ 6\sqrt{3 } }{ 3 }=2\sqrt{ 3 }$
$GH=6-2\sqrt{ 3 }$ (cm)

（3）
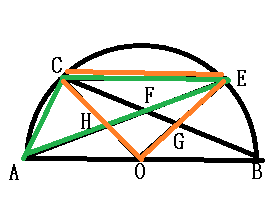
平行線を利用した等積変形の理解が試される問題です。
等積変形を緑から黄色に一回だけ行い、正三角形FOBの高さを三平方の定理で求め⊿AFOの面積を、おうぎ形ODAから正三角形DAOの面積をひいて 弧ADと弦ADに囲まれた面積を、だすことで求めることもできますが、それでは計算が厄介です。
黄色がさらに等積変形でオレンジの三角形になることに気づけるとおうぎ形の面積を出すことだけで答えが導けます。

弧FGと弦FGで囲まれた部分は弧CAと弦CAで囲まれた部分の面積と同じ。-①
半円が６等分されていますから、弧GB上の中心角∠GOB＝30°
弧FB上の中心角∠FOB＝180°÷6×2＝60°ですから、円周角∠FAB＝30°
このことから、FA//GO-②
∠DOA＝180°÷6×2＝60°。
⊿ODBはOD=OBの二等辺三角形で書くDBO＝∠DOA÷2＝180÷6×2÷2＝30°＝∠BDO、また、∠BDF＝∠FOB÷2＝60°÷2＝30°。
したがって、∠ODF=60°
これによりDF // AB-③
②から、FAを底辺に見た⊿GFAは等積変形により⊿OFAと面積が同じ。
③から、AOを底辺に見た⊿OFAは等積変形により⊿DAOと面積が同じ。-④
①と④から、件の面積の和はおうぎ形ODAの面積と同じになります。
$\displaystyle 6^2π×\frac{ 60 }{ 360 }=\frac{ 6×6π }{ 6 }=6π（㎤）$