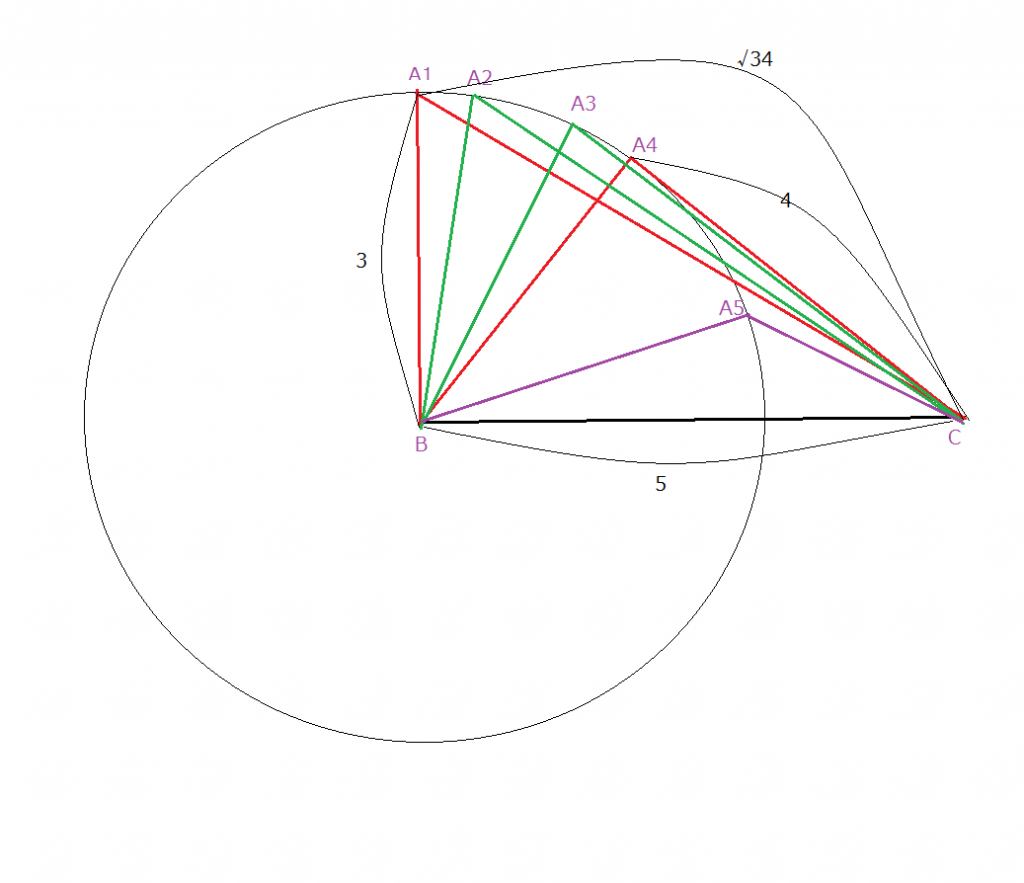
中心Bの円の半径を3、Aは円の円周を$A_1からA_5$まで移動する
ものとし、 BC=5とする。∠CはAB=3で最大辺ではないためAC
がいかなる長さをとろうが 常に鋭角である。赤は直角三角形
($⊿A_1BC$は∠B=90°、$⊿A_4BC$は ∠A=90°)
緑は鋭角三角形、紫は鈍角三角形である。
Aが円周上の$\mathrm{ A }_1$の位置にあるとき、三平方の定理から、
$\mathrm{ A }_1C^2= \mathrm{ A }_1B^2+BC^2$
∠Bが鋭角になるのは、 $\mathrm{ A }_1$ が円周上を右に移動して、例えば $\mathrm{ A }_2$ の位置に来た時である。
このとき、図から $\mathrm{ A }_2C< \mathrm{ A }_1C$は明らかだから、
$\mathrm{ A }_2C^2< \mathrm{ A }_1C^2 =\mathrm{ A }_1B^2+BC^2$
即ち、$\mathrm{ A }_2C^2< 3^2+5^2=34$
したがって、$AC<\sqrt{ 34 }$のとき∠Bは鋭角になる。-①
$また、\mathrm{ A }_4の位置で∠B \mathrm{ A }_4C=90°になり、$
$\mathrm{ A }_4C^2=BC^2- \mathrm{ A }_4B^2$
$A_4$の手前の$A_3$では図から$A_3C>A_4C$は明らかだから、
$A_3C^2$>$A_4C2$=$BC^2$-$A_4B^2$=$5^2-3^2$=25-9=16
したがって、AC>4のとき∠Cは鋭角になる。 -②
①と②からこの⊿ABCが鋭角三角形となるのは、$4<AC<\sqrt{ 34 }$のとき
即ち、 $4<x<\sqrt{ 34 } $