第1問
[1]
(1)
半径2、弧長3の扇型の中心角は、$2π(=360°)×\displaystyle \frac{ 3 }{ 4π }(弧長:全周)=$$\displaystyle \frac{ 3 }{ 2 }=\mathrm{ θ }_a$
半径3、弧長9の扇型の中心角は、$2π×\displaystyle \frac{ 9 }{ 6π }=3=\mathrm{ θ }_b$
1ラジアンは半径1、弧長1の中心角で$1=\mathrm{ θ }_c$
よって、$\mathrm{ θ }_c<\mathrm{ θ }_a<\mathrm{ θ }_b$
(2)
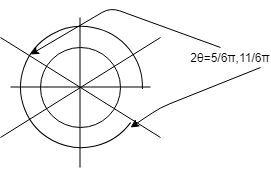
$\cos 2\theta=\cos (2\theta+\displaystyle \frac{ π }{ 3 })$
単位円で考えると、コサインはx座標の値だから、
$\cos 2\theta$と$\cos (2\theta+\displaystyle \frac{ π }{ 3 })$の値が同じになるとき、
$2\theta$と$2\theta+\displaystyle \frac{ π }{ 3 }$はエックス軸とのなす角がそれぞれ等しい。
これらのことから、$2\theta$の値を0≦2θ≦2π(与えられた条件0≦θ≦πの各辺を2倍する)の範囲で探すと、$2θ=\displaystyle \frac{ 5π }{ 6 },\displaystyle \frac{ 11π }{ 6 }$
したがって、$θ=\displaystyle \frac{ 5π }{ 12 },\displaystyle \frac{ 11π }{ 12 }$
$\cos 2\theta=\cos (2\theta+\displaystyle \frac{ π }{ 3 })=\cos (3\theta+α)$は連立方程式だから、$\cos 2\theta=\cos (3\theta+α)$が成り立ち、0≦θ≦πでの解は上で求めたように
$θ=\displaystyle \frac{ 5π }{ 12 },\displaystyle \frac{ 11π }{ 12 }$である。
解を求めるθの範囲を-π<θ<πに広げると、$θ=\displaystyle -\frac{ 7π }{ 12 },\displaystyle -\frac{ π }{ 12 },\displaystyle \frac{ 5π }{ 12 },\displaystyle \frac{ 11π }{ 12 }$である。
これを$\cos 2\theta=\cos (3\theta+α)$に一つ一つ代入して$\mathrm{ α }_1,\mathrm{ α }_2,\mathrm{ α }_3$を求める。
$\displaystyleθ=-\frac{ 7π }{ 12 }$のとき、$-\frac{ 7π }{ 6 }=3×-\frac{ 7π }{ 12 }+α$から、$α=\frac{ 21π }{ 12 }-\frac{ 14π }{ 12 }=\frac{ 7π }{ 12 }$-①
$\displaystyleθ=-\frac{ π }{ 12 }$のとき、$-\frac{ π }{ 6 }=3×-\frac{ π }{ 12 }+α$から、$α=\frac{ 3π }{ 12 }-\frac{ 2π }{ 12 }=\frac{ π }{ 12 }$-②
$θ=\displaystyle\frac{ 5π }{ 12 }$のとき、$\frac{ 5π }{ 6 }=3×\frac{ 5π }{ 12 }+α$から、$α=-\frac{ 15π }{ 12 }+\frac{ 10π }{ 12 }=-\frac{ 5π }{ 12 }$-③
$θ=\displaystyle\frac{ 11π }{ 12 }$のとき、$\frac{ 11π }{ 6 }=3×\frac{ 11π }{ 12 }+α$から、$α=-\frac{ 33π }{ 12 }+\frac{ 22π }{ 12 }=-\frac{ 11π }{ 12 }$-④
ただし、上記4つのαにつき、$\cos x=\cos (-x)$であることを考慮に入れると、
$α=±\displaystyle\frac{ 7π }{ 12 },±\frac{ π }{ 12 },±\frac{ 5π }{ 12 },±\frac{ 11π }{ 12 }$である。
例えば、③の場合、$\cos \frac{ 5π }{ 12 }=\cos (-\frac{ 5π }{ 12 })$であるから、
$-\frac{ 5π }{ 6 }=3×-\frac{ 5π }{ 12 }+α$を満たすαも方程式の解である。
この時、$α=\frac{ 15π }{ 12 }-\frac{ 10π }{ 12 }=\frac{ 5π }{ 12 }$であり、同様に、①②④の値に逆符号がついた値もα解である。
α>0から、$\mathrm{ α }_1=\displaystyle \frac{ π }{ 12 }, \mathrm{ α }_2=\displaystyle \frac{ 5π }{ 12 }, \mathrm{ α }_3=\displaystyle \frac{ 7π }{ 12 }$である。
[2]
① $\log_{ 4 } xy≧\log_{ 2 } y+1$
$\displaystyle \frac{ \log_{ 2 } xy }{ \log_{ 2 } 4 }≧\log_{ 2 } y+\log_{ 2 } 2$
$\displaystyle \frac{ 1 }{ 2 } \log_{ 2 } xy≧\log_{ 2 } 2y$
$\displaystyle \log_{ 2 } (xy)^ \frac{ 1 }{ 2 }≧\log_{ 2 } 2y$
$\displaystyle (xy)^ \frac{ 1 }{ 2 }≧2y$
$\displaystyle \sqrt{ xy }≧2y$
x>0,y>0から、$xy≧4y^2$
y≠0から、x≧4y
y>0から、$\displaystyle 0<y≦ \frac{ y }{ 4 }$
② $\displaystyle 4^{x-1}+8≦9・2^{x-1}$
$\displaystyle 4^{x-1}=(2^2)^{x-1}=2^{2x-2}=2^{2x}・2^{-2}= \frac{ 1 }{ 4 }(2^x)^2$
$\displaystyle 2^{x-1}=2^x・2^{-1}= \frac{ 1 }{ 2 }・2^x$
したがって、
与式=$\displaystyle \frac{ 1 }{ 4 }・(2^x)^2-9・\frac{ 1 }{ 2 }・2^x+8$
$=\displaystyle (2^x)^2-18・2^x+32$
$=\displaystyle (2^x-2)(2^x-16)≦0$
$(2^x-2)(2^x-16)$は2^xの2次関数だから、$2≦2^x≦16$
1≦x≦4
領域$y≦\frac{ 1 }{ 4 }x$,1≦x≦4の範囲内で、整数m,nを用いて$x=2^m,y=2^n$と表せる点を考える。
この場合、まず該当するx座標は$2^0=1,2^1=2,2^2=4$だけである。
x座標が$2^0=1$のとき、yの最大値は$y=\frac{ 1 }{ 4 }x$上の点で
$\frac{ 1 }{ 4 }=2^{-2}$である。
更にyの値が小さくになるに従い、$2^{-3},2^{-4},2^{-5}$…とyの値は無数に存在する。
x座標が$2^1=2$のとき、yの最大値は$y=\frac{ 1 }{ 4 }x$上の点で$\frac{ 1 }{ 2 }=2^{-1}$である。
更にyの値が小さくになるに従い、$2^{-2},2^{-3},2^{-4}…$とyの値は無数に存在する。
x座標が$2^2=4$のとき、yの最大値は$y=\frac{ 1 }{ 4 }x$上の点で
$\displaystyle 1=2^0$である。
更にyの値が小さくになるに従い、&2^{-1},2^{-2},2^{-3}$…とyの値は無数に存在する。
よって、yの値で考えると、$2^0×1個,2^{-1}×2個,2^{-2}×3個,2^{-3}×3個$で点の数は9個となり、
$2^{-4}$からは10個以上となる。
したがって、y>kを満たす点が10個以下となるkの値は$2^{-4}=\frac{ 1 }{ 16 }$である。
同じ領域内で$y=\frac{ 1 }{ 100 }x$を満たす$x=2^m,y=2^n$(m,nは整数)の組を考えると、
①$x=2^0=1$のとき、$\frac{ 1 }{ 2^7 }<\frac{ 1 }{ 100 }<\frac{ 1 }{ 2^6 }$だから、$
$y≧\frac{ 1 }{ 100 }x$を満たすyの最小値は$2^{-6}$である。
したがって、$x=2^0=1$のとき、$\frac{ 1 }{ 100 }x≦y≦\frac{ 1 }{ 4 }x$を満たすyの値は$2^{-6}から2^{-2}$までの5個。
②$x=2^1=2$のとき、$\frac{ 1 }{ 2^6 }<\frac{ 1 }{ 50 }<\frac{ 1 }{ 2^5 }$だから、
$y≧\frac{ 1 }{ 100 }x$を満たすyの最小値は$2^{-5}$である。
たがって、$x=2^1=2$のとき、$\frac{ 1 }{ 100 }x≦y≦\frac{ 1 }{ 4 }x$を満たすyの値は$2^{-5}から2^{-1}$までの5個。
③$x=2^2=4$のとき、$\frac{ 1 }{ 2^5 }<\frac{ 1 }{ 25 }<\frac{ 1 }{ 2^4 }$だから、
$y≧\frac{ 1 }{ 100 }x$を満たすyの最小値は$2^{-4}$である。
したがって、$x=2^1=2$のとき、$\frac{ 1 }{ 100 }x≦y≦\frac{ 1 }{ 4 }x$を満たすyの値は$2^{-4}$から$2^0$までの5個。
①+②+③=15個
第2問
ア
直線ABの傾きは、$A(a,a^2),B(b,b^2)$を通ることから、
$\frac{ b^2-a^2 }{ b-a }=\frac{ (b-a)(b+a) }{ b-a }=a+b$
今傾きが1だからa+b=1
イウ
Aから引いたx軸との平行線とBから引いたy軸との平行線の交点をOとすると、
ABの傾きが1だから∠OAB=45°、AO=BO
したがって、$AB:AO=3\sqrt{ 2 }:AO=\sqrt{ 2 }:1$からAO=3=$b-a$
a+b=1,$-a+b=3$の連立方程式を解いて、加減法でa=-1,b=2
エオ
$\mathrm{ C }_2:y=-2x^2+px+q$がA(-1,1),B(2,4)を通ることから、
$-2(-1)^2+(-1)p+q=1$,$-2(2)^2+2p+q=4$の連立方程式を解いて、p=3,q=6
即ち、$y=-2x^2+3x+6 $ ここまで
カキクケコ
グラフの形状から、x=2の前後で二つの曲線のyの値の大小が逆転するので、$S=\int_k^2 \{ (-2x^2+3x+6)-x^2 \} dx$$+\int_2^{k+2} \{ x^2-(2x^2+3x+6) \} dx $
=$\int_k^2 \{ (-2x^2+3x+6)-x^2 \} dx$$-\int_2^{k+2} \{ -x^2+(2x^2+3x+6) \} dx $
=$\left[ -x^3+\frac{ 3 }{ 2 }x^2+6x \right]$$_k^2-\left[ -x^3+\frac{ 3 }{ 2 }x^2+6x \right]_2^{k+2}$
=$2(-2^3+ \frac{ 3 }{ 2 }・2^2+6・2)-(-k^3+\frac{ 3 }{ 2 }k^2+6k)$$-\{ -(k+2)^3+\frac{ 3 }{ 2 }(k+2)^2+6(k+2) \}$
=$10+k^3- \frac{ 3 }{ 2 }k^2-6k-(-k^3-6k^2-12k$$-8+\frac{ 3 }{ 2 }k^2+6k+6+6k+12)$
=$20+k^3- \frac{ 3 }{ 2 }k^2-6k+k^3+6k^2$$+12k+8- \frac{ 3 }{ 2 }k^2-6k-6-6k-12$
=$20+k^3- \frac{ 3 }{ 2 }k^2-6k+k^3+6k^2$$+12k+8- \frac{ 3 }{ 2 }k^2-6k-6-6k-12$
=$2k^3+3k^2-6k+10$
サシス
3次式Sのグラフの極値を考える。
$2k^3$の係数3は正だからこのグラフは下から上がってきて、
極大値に達した後でいったん下降し、極小値に達した後で再度上昇する。
極値の$x$座標における傾きは0であるから、微分してその時の$x$座標を求める。
$S’=6k^2+6k-6=6(k^2+k-1)$
$6(k^2+k-1)=0$の解は、解の公式から$k= \frac{ -1±\sqrt{ 1+4 } }{ 2 }=\frac{ -1±\sqrt{ 5 } }{ 2 }$
したがって、$S’=6(k- \frac{ -1+\sqrt{ 5 } }{ 2 })(k- \frac{ -1-\sqrt{ 5 } }{ 2 })$
から、極大値は $\frac{ -1-\sqrt{ 5 } }{ 2 }$におけるyの値、極小値は$\frac{ -1+\sqrt{ 5 } }{ 2 }$ におけるyの値である。
ここで、$ \frac{ -1-\sqrt{ 5 } }{ 2 }<0<\frac{ -1+\sqrt{ 5 } }{ 2 }<2$であるから、
Sが最小になるときのkの値は$\frac{ -1+\sqrt{ 5 } }{ 2 }$である。
セソタ
Bを通る直線が$\mathrm{ C }_1,\mathrm{ C }_2,x≧0$で囲まれている(=封じ込められた)部分を2分割するのは、
Bにおける$\mathrm{ C }_2$の接線の傾きよりも大きくて、Bにおける$\mathrm{ C }_1$の接線の傾きより小さい時である。
前者は-4(2)+3=-5,後者は2(2)=4であるから、-5<m<4。
チツ
$\mathrm{ C }_1,\mathrm{ C }_2,x≧0$で囲まれている(=封じ込められた)部分の面積は
$S=2k^3+3k^2-6k+10$のkに0を代入した時のSの値であり、10である。
線分OBと$\mathrm{ C }_1$に囲まれた面積は、
$\int_0^2 ( 2x-x^2 )=\left[ – \frac{ 1 }{ 3 }x^3+x^2 \right]_0^2$
$- \frac{ 1 }{ 3 }(2^3)+2^2=\frac{ -8+12 }{ 3 }= \frac{ 4 }{ 3 }$
Bを通る直線lのy切片をRとすると、直線lによって領域Eが2等分されるならば、
$⊿RBO+\frac{ 4 }{ 3 }=\frac{ 10 }{ 2 }=5$が成り立つから、
$⊿RBO=\frac{ 11 }{ 3 }$
ORを底辺と考えると、高さは2だから、$OR×2×\frac{ 1 }{ 2 }=\frac{ 11 }{ 3 }
$
$OR=\frac{ 11 }{ 3 }$から直線lは(0,$\frac{ 11 }{ 3 }$),(2,4)を通る直線である。
よって、
$y=\frac{ 4-\displaystyle \frac{ 11 }{ 3 } }{ 2 }x+ \frac{ 11 }{ 3 }$
=$ \frac{ 1 }{ 6 }x+ \frac{ 11 }{ 3 }$
したがって、$m= \frac{ 1 }{ 6 }$
